参考链接：

二分查找

二分查找（Binary Search）是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

二分查找的基本步骤（基础版）：

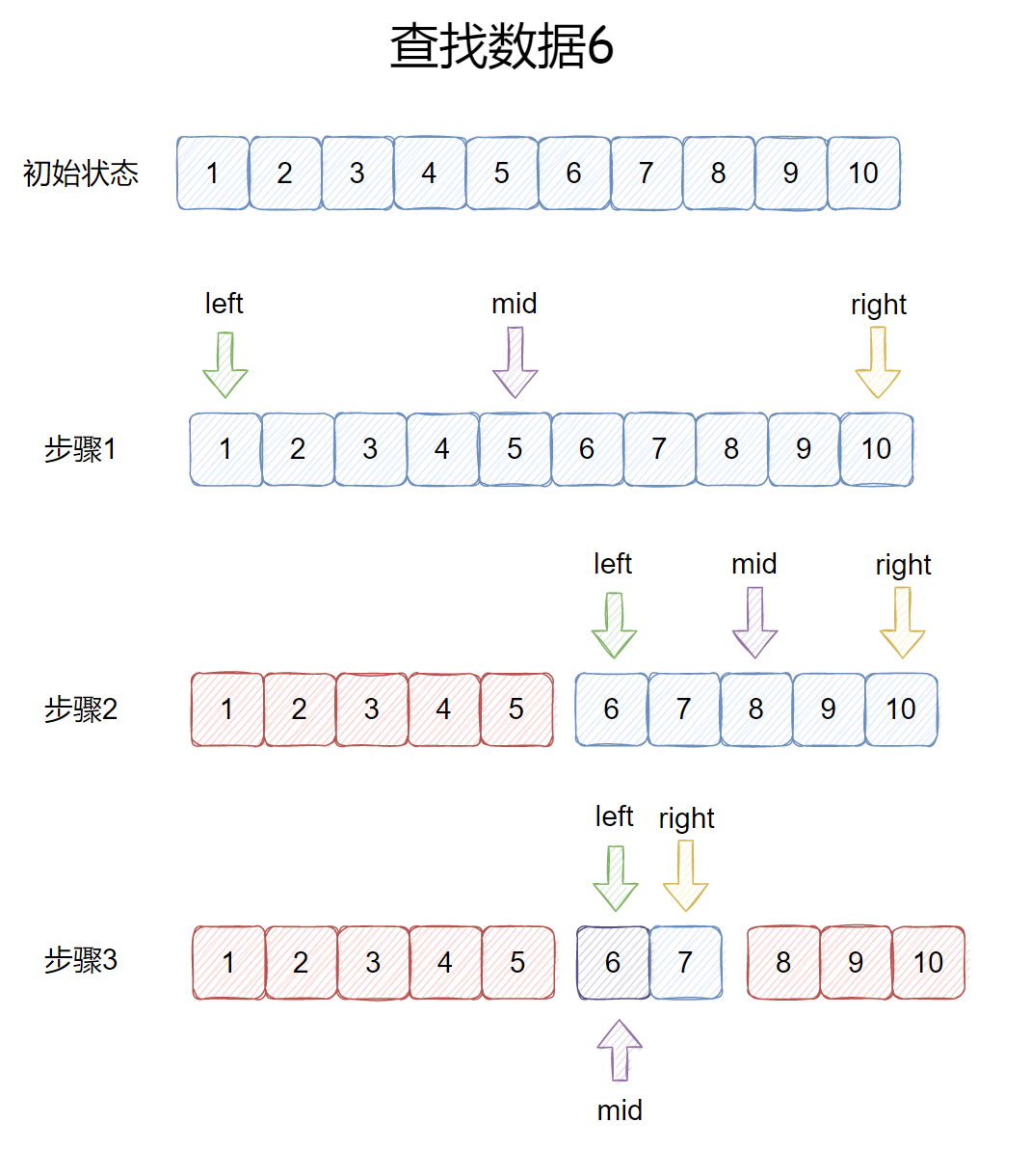
  1. 确定搜索范围：初始化两个指针，确定整个有序数组的搜索范围，即左边界和右边界。通常初始时左边界为数组的第一个元素索引（left = 0），右边界为数组的最后一个元素索引 （right = len(array) - 1）。
  2. 检查基本条件：如果 left > right，说明搜索范围为空，元素不存在于数组中，直接返回。
  3. 计算中间索引：使用 mid = (left + right) >>> 1 来避免整数溢出，并确定中间元素的索引。
  4. 比较中间元素：如果中间元素正好是要查找的元素，则返回中间元素的索引。
  5. 缩小搜索范围：如果中间元素大于要查找的元素，说明要查找的元素（如果存在）一定在左半部分，因此更新 right = mid - 1。如果中间元素小于要查找的元素，说明要查找的元素（如果存在）一定在右半部分，因此更新 left = mid + 1。
  6. 重复步骤2-5：直到找到元素或搜索范围为空。
二分查找基础版

二分查找法的关键之处在于每一步都将搜索范围减半，因此它的时间复杂度为 O(log n)，其中 n 是数组中元素的数量。相较于线性搜索的 O(n) 时间复杂度，二分查找法在大型有序数组中能够显著提高搜索效率。

二分查找法有一定的前提条件：数组为有序数组，同时题目还强调 数组中无重复元素。如果数组无序，需要先进行排序操作，这会增加额外的时间复杂度。一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的。另外，在特定情况下，二分查找法可能不如其他算法高效，例如对于小规模数据或者频繁插入/删除元素的数据结构。

大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即 [i, j]，或者左闭右开即 [i, j) 。由此也衍生出许多其他版本。

基础版

第一种写法，我们定义 target 是在一个在 左闭右闭 的区间里，也就是 [i, j] 。

区间的定义这就决定了二分法的代码应该如何写，因为定义 target 在 [i, j] 区间，所以有如下两点：

  • while (i<= j) 要使用 <= ，而不是 i < j ，因为 i == j 是有意义的。

    • i == j 意味着 i，j 它们指向的元素也会参与比较。
    • i < j 只意味着 m 指向的元素参与比较。

  • if (a[m] > target) ，j 要赋值为 m - 1，因为当前这个 a[m] 一定不是target，那么接下来要查找的左区间结束下标位置就是 m - 1 。

例如在下列数组中查找元素9，如图所示：

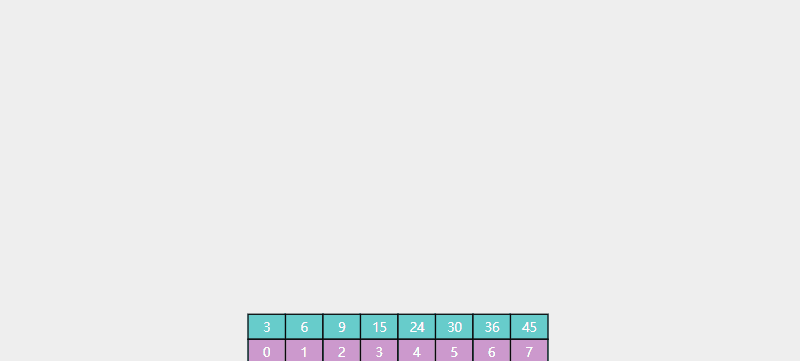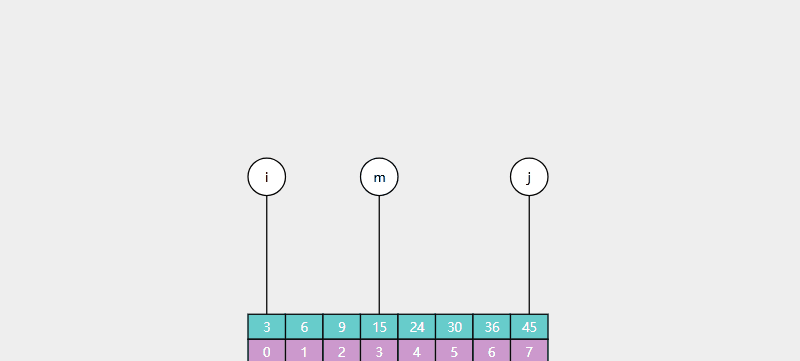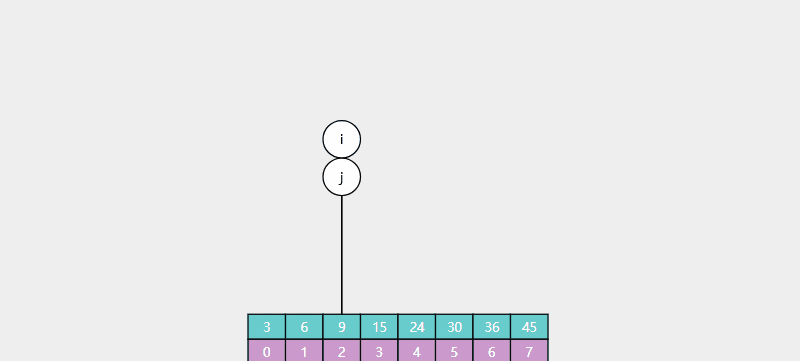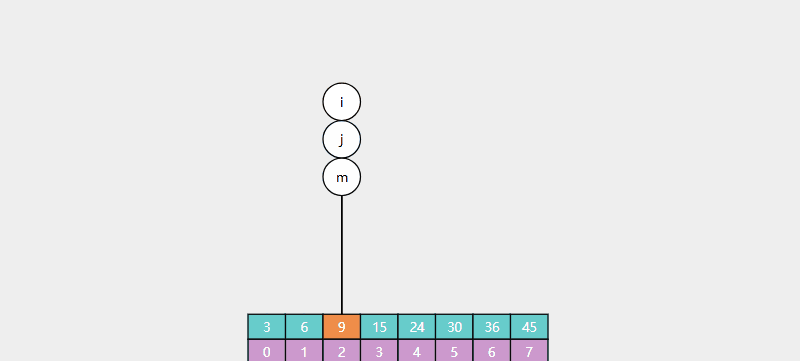
二分查找基础版

java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static int binarySearchBasic(int[] a, int target) {
    int i = 0, j = a.length - 1;            // 设置指针和初值，定义target在左闭右闭的区间里[i, j]
    // L 次  元素在最左边 L 次，  元素在最右边 2*L 次
    while (i <= j) {                        // 当i==j，区间[i, j]依然有效，所以用 <=
        int m = (i + j) >>> 1;              // 防止溢出 等同于(i + j)/2
        if (target < a[m]) {
            j = m - 1;                      // target 在左区间，所以[j, m - 1]
        } else if (a[m] < target) {
            i = m + 1;                      // target 在右区间，所以[m + 1, j]
        } else {
            return m;                       // 数组中找到目标值，直接返回下标
        }
    }
    // 未找到目标值
    return -1;
}

求中间值下标的语句，采用 int m = (l + r) >>> 1 的写法而不用 int m = (l + r) / 2 是为了防止溢出。详见文末 提前溢出 。

改动版

如果说定义 target 是在一个在 左闭右开 的区间里，也就是 [i, j) ，那么二分法的边界处理方式则截然不同。

有如下两点：

  • while (i< j)，这里使用 < ，因为 i == j 在区间 [i, j) 是没有意义的

    • i == j，在 [i, j) 是无效的空间，所以使用 < 。

  • if (a[m] > target) ，j 更新为 m，因为当前 a[m] 不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以 j 更新为m，即：下一个查询区间不会去比较 a[m] 。

例如在下列数组中查找元素16，如图所示：

二分查找改动版

java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int binarySearchAlternative(int[] a, int target) {
    int i = 0, j = a.length;     // 第一处，定义target在左闭右开的区间里，即：[i, j)
    while (i < j) {              // 第二处，i == j，在[i, j)是无效的空间，所以使用 <
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m;               // 第三处，target 在左区间，在[i, j)中
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            return m;
        }
    }
    return -1;
}

平衡版

思想：

  1. 左闭右开的区间，也就是 [i, j) ，i 指向的可能是目标，而 j 指向的不是目标。
  2. 不奢望循环内通过 m 找出目标，缩小区间直至剩 1 个，剩下的这个可能就是要找的（通过 i ）。
    • j - i > 1 的含义是，在范围内待比较的元素个数 > 1 。
  3. 改变 i 边界时，它指向的可能是目标，因此不能 m+1 。
  4. 循环内的平均比较次数减少了。
  5. 时间复杂度 O(log(n)) 。

例如在下列数组中查找元素18，如图所示：

二分查找平衡版

java代码：

1
2
3
4
5
6
7
8
9
10
11
12
public static int binarySearchBalance(int[] a, int target) {
    int i = 0, j = a.length;
    while (1 < j - i) {         // 范围内待查找的元素个数 > 1 时
        int m = (i + j) >>> 1;
        if (target < a[m]) {    // 目标在左边
            j = m;
        } else {                // 目标在 m 或右边
            i = m;
        }
    }
    return (target == a[i]) ? i : -1;
}

Java 源码版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private static int binarySearch0(long[] a, int fromIndex, int toIndex,
                                     long key) {
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        long midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}
  • 例如 [1,3,5,6] 要插入 2 ，那么就是找到一个位置，这个位置左侧元素都比它小。
    • 等循环结束，若没找到，low 左侧元素肯定都比 target 小，因此 low 即插入点。
  • 插入点取负是为了与找到情况区分。
  • -1 是为了把索引 0 位置的插入点与找到的情况进行区分。

Leftmost 与 Rightmost

有时我们希望返回的是最左侧的重复元素，如果用 Basic 二分查找：

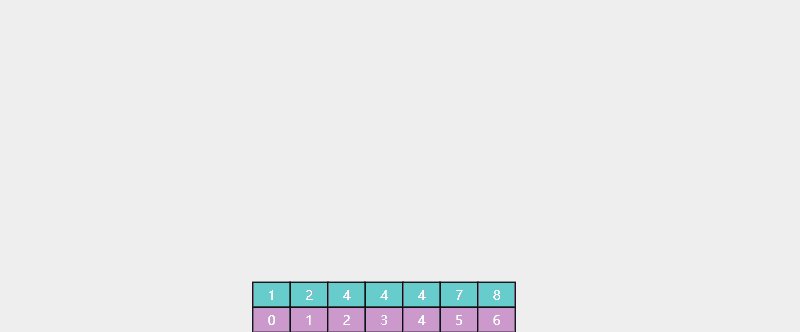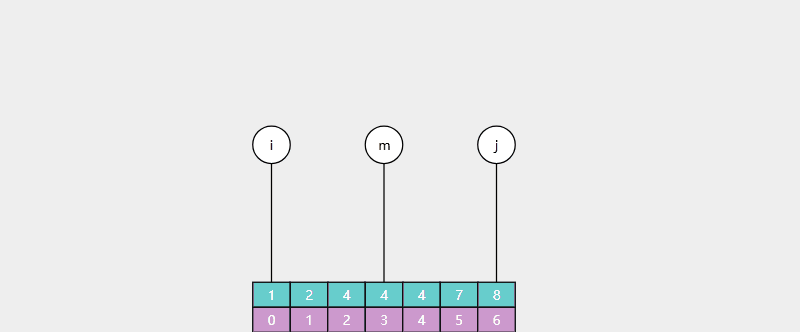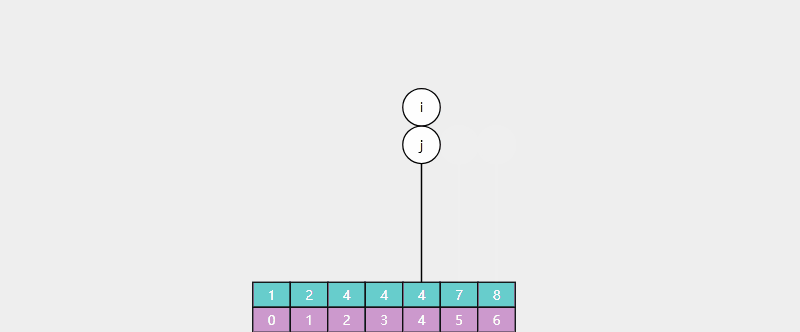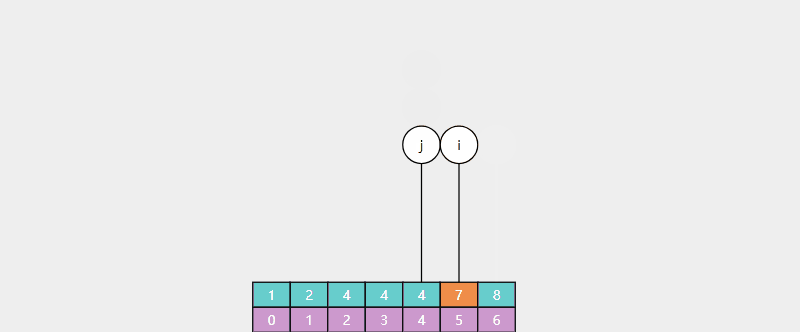
  • 对于数组 [1, 2, 3, 4, 4, 5, 6, 7]，查找元素4，结果是索引3 。

  • 对于数组 [1, 2, 4, 4, 4, 5, 6, 7]，查找元素4，结果也是索引3，并不是最左侧的元素。

使用 Leftmost 查找：

  • 找到目标点后，记录点为候选位置。
  • 然后向左缩小查找范围，查看是否有更靠左的目标点。
  • 没有更靠左的目标点，候选位置即为最左侧的重复元素。

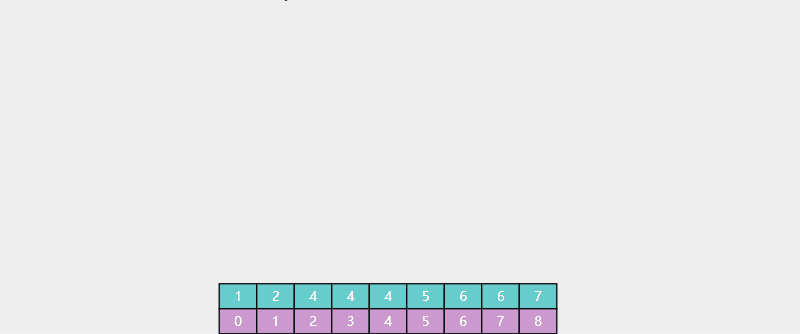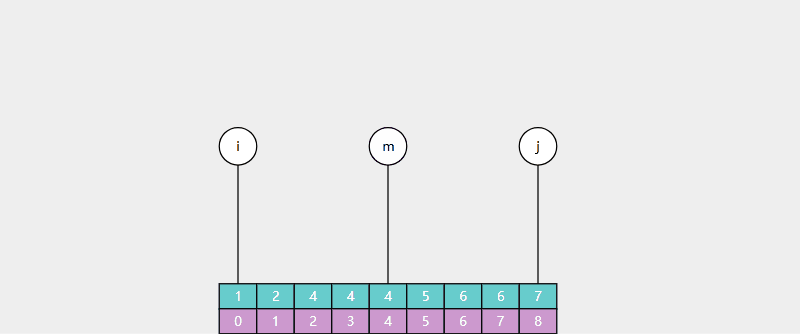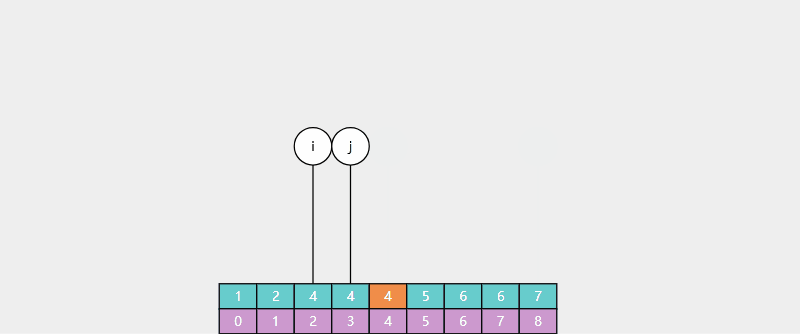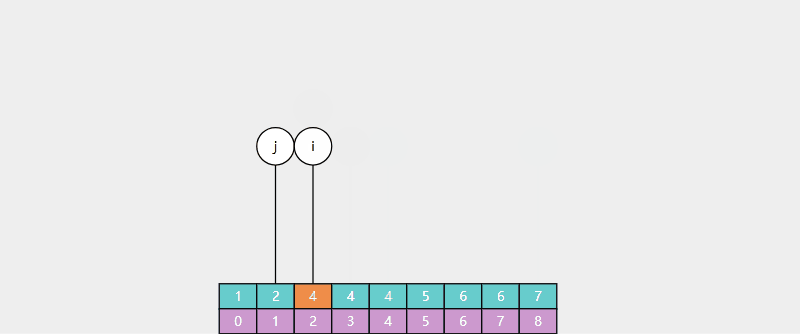
二分查找Leftmost

java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static int binarySearchLeftmost1(int[] a, int target) {
    int i = 0, j = a.length - 1;
    int candidate = -1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            candidate = m; // 记录候选位置
            j = m - 1;     // 继续向左
        }
    }
    return candidate;
}

如果希望返回的是最右侧元素：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static int binarySearchRightmost1(int[] a, int target) {
    int i = 0, j = a.length - 1;
    int candidate = -1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            candidate = m; // 记录候选位置
            i = m + 1;	   // 继续向右
        }
    }
    return candidate;
}

应用

对于 Leftmost 与 Rightmost，可以返回一个比 -1 更有用的值。

Leftmost 返回的 i 代表 >= target 的最靠左索引：

  • target 存在：返回值代表 = target 的最靠左索引。
  • target 不存在：返回值代表 > target 的最靠左索引。

例：查找 4（存在），返回值 i = 2，对应 4 的最靠左索引

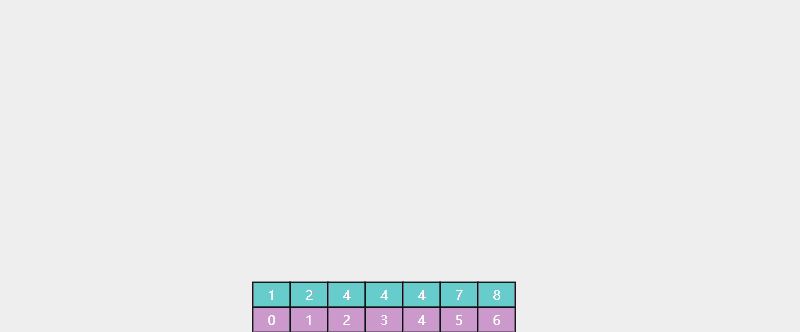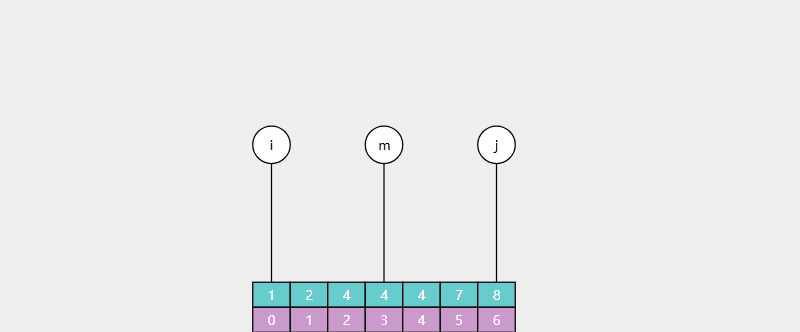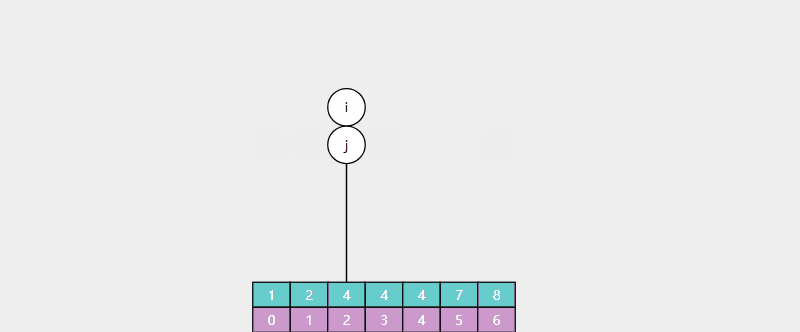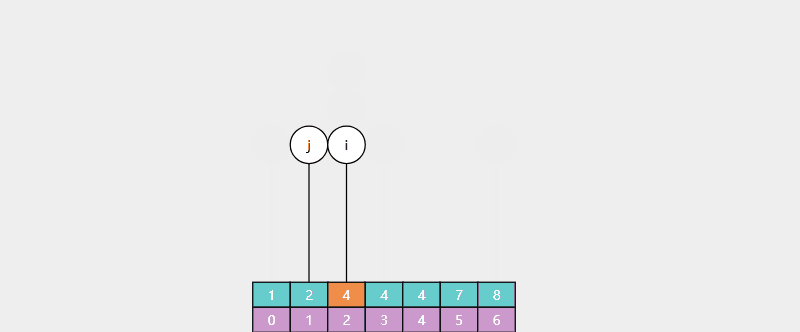
二分查找Leftmost2 target存在

例：查找 5（不存在），返回值 i = 5，对应 > 4 的最靠左索引（7 的索引）

二分查找Leftmost2 target不存在

java代码：

1
2
3
4
5
6
7
8
9
10
11
12
public static int binarySearchLeftmost(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target <= a[m]) {
            j = m - 1;
        } else {
            i = m + 1;
        }
    }
    return i; 
}
  • leftmost 返回值 i 的另一层含义 < target 的元素个数。
  • 小于等于中间值，都要向左找。

Rightmost 返回的 i - 1 代表 <= target 的最靠右索引：

  • target 存在：返回值代表 = target 的最靠右索引。
  • target 不存在：返回值代表 < target 的最靠右索引。
1
2
3
4
5
6
7
8
9
10
11
12
public static int binarySearchRightmost(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else {
            i = m + 1;
        }
    }
    return i - 1;
}
  • 大于等于中间值，都要向右找。

几个名词

几个名词

范围查询：

  • 查询 x < 4，0 .. leftmost(4) - 1
  • 查询 x <= 4，0 .. rightmost(4)
  • 查询 4 < x，rightmost(4) + 1 .. ∞
  • 查询 4 <= x， leftmost(4) .. ∞
  • 查询 4 <= x <= 7，leftmost(4) .. rightmost(7)
  • 查询 4 < x < 7，rightmost(4) + 1 .. leftmost(7) -1

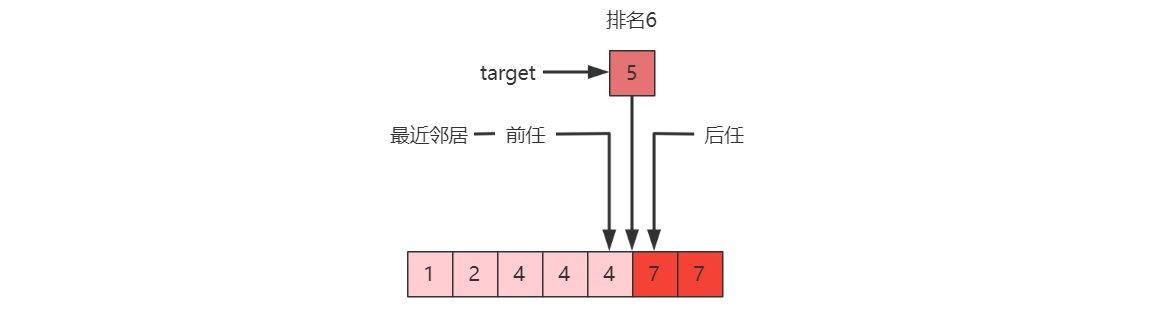
求排名：leftmost(target) + 1

  • target 可以不存在，如：leftmost(5) + 1 = 6
  • target 也可以存在，如：leftmost(4) + 1 = 3

求前任（predecessor）：leftmost(target) - 1

  • leftmost(3) - 1 = 1，前任 a - 1 = 2
  • leftmost(4) - 1 = 1，前任 a - 1 = 2

求后任（successor）：rightmost(target)+1

  • rightmost(5) + 1 = 5，后任 a - 5 = 7
  • rightmost(4) + 1 = 5，后任 a - 5 = 7

求最近邻居：

  • 前任和后任距离更近者

拓展阅读

提前溢出

关于求中间值坐标的写法。

  • 最简单的写法是 m=(i+j)/2，但直接相加会使得 i+j 大于 2^31^−1(2147483647) 时（提前）溢出，例如 i=1，j=2^31^−1，计算 m 时，i+j=2^31^(2147483648) 导致溢出。但原本应该有 m=1073741824，i，j，m 都不应该溢出，只是因为 i+j 导致了（提前）溢出。
  • 可以写成先减后加的形式 m=i+(j−i)/2。这是较常见的形式。
  • 用 >> 代替除法，写成 m=i+((j−i)>>1) 也是可以的。
  • 这里采用 JDK 中采用的 m=(i+j)>>>1 写法。
    • >>> 是无符号右移运算符 (Unsigned right shift operator) ，与 >> 的区别在于右移的时不考虑符号位，总是从左侧补 0，i + j 不溢出的时候符号位本来就是0，与 >> 效果相同。 i+j 溢出时最高位符号位从 0 进位成了 1，经过 >>> 的移位，最高位又变回了 0，这是一种利用位运算的 trick，可以参考这里。
    • 需要注意的是若采用此种写法，要保证 (i+j) 为非负整数 。因为若 (i+j) 为负数，经过高位补 0 后将得到错误的正数。通常情况下，i 与 j 代表下标，不会出现负数情况，但有的题目要在包含正负数的范围内，对这些 「数值」（而非下标） 进行二分查找， i 和 j 表示可能为正也可能为负的「数值」，此时就不用能 >>> 的写法。例如 462. 最少移动次数使数组元素相等 II 题就不能采用 >>> 写法。